Geometria Espacial

Pirâmide

Consideremos um polígono contido em um plano (por exemplo, o plano horizontal) e um ponto V localizado fora desse plano. Uma Pirâmide é a reunião de todos os segmentos que têm uma extremidade em P e a outra num ponto qualquer do polígono. O ponto V recebe o nome de vértice da pirâmide.

Elementos de uma pirâmide

Em uma pirâmide, podemos identificar vários elementos:

1.Base: A base da pirâmide é a região plana poligonal sobre a qual se apoia a pirâmide.

2.Vértice: O vértice da pirâmide é o ponto isolado P mais distante da base da pirâmide.

3.Eixo: Quando a base possui um ponto central, isto é, quando a região poligonal é simétrica ou regular, o eixo da pirâmide é a reta que passa pelo vértice e pelo centro da base.

4.Altura: Distância do vértice da pirâmide ao plano da base.

5.Faces laterais: São regiões planas triangulares que passam pelo vértice da pirâmide e por dois vértices consecutivos da base.

6.Arestas Laterais: São segmentos que têm um extremo no vértice da pirâmide e outro extremo num vértice do polígono situado no plano da base.

7.Apótema: É a altura de cada face lateral.

8.Superfície Lateral: É a superfície poliédrica formada por todas as faces laterais.

9.Aresta da base: É qualquer um dos lados do polígono da base.

Classificação das pirâmides pelo número de lados da base:

triangular

base:triângulo

quadrangular

base:quadrado

pentagonal

base:pentágono

hexagonal

base:hexágono

Àrea da Pirâmide

Às vezes podemos construir fórmulas para obter as áreas das superfícies que envolvem um determinado sólido. Tal processo é conhecido como a planificação desse sólido. Isto pode ser realizado se tomarmos o sólido de forma que a sua superfície externa seja feita de papelão ou algum outro material.

No caso da pirâmide, a idéia é tomar uma tesoura e cortar (o papelão d)a pirâmide exatamente sobre as arestas, depois reunimos as regiões obtidas num plano que pode ser o plano de uma mesa.

As regiões planas obtidas são congruentes às faces laterais e também à base da pirâmide.

Se considerarmos uma pirâmide regular cuja base tem n lados e indicarmos por A(face) a área de uma face lateral da pirâmide, então a soma das áreas das faces laterais recebe o nome de área lateral da pirâmide e pode ser obtida por:

A(lateral) = n A(face)

Volume da Pirâmide

O volume de uma pirâmide pode ser obtido como um terço do produto da área da base pela altura da pirâmide, isto é:

Volume = (1/3) A(base) h

Cilindro

As características apresentadas antes para cilindros circulares, são também possíveis para outros tipos de curvas diretrizes, como: elipse, parábola, hipérbole, seno ou outra curva simples e suave num plano. Mesmo que a diretriz não seja uma curva conhecida, ainda assim existem cilindros obtidos quando a curva diretriz é formada por uma reunião de curvas simples. Por exemplo, se a diretriz é uma curva retangular, temos uma situação patológica e o cilindro recebe o nome especial de prisma.

Em função da curva diretriz, o cilindro terá o nome de cilindro: elíptico, parabólico, hiperbólico, sinuzoidal (telha de eternit).

O conceito de cilindro é muito importante. Nas cozinhas encontramos aplicações intensas do uso de cilindros. Nas construções, observamos caixas d'água, ferramentas, objetos, vasos de plantas, todos eles com formas cilíndricas.

Existem outras formas cilíndricas diferentes das comuns, como por exemplo o cilindro sinuzoidal obtido pela translação da função seno.

Elementos de um Cilindro

Em um cilindro, podemos identificar vários elementos:

1.Base: É a região plana contendo a curva diretriz e todo o seu interior. Num cilindro existem duas bases.

2.Eixo: É o segmento de reta que liga os centros das bases do "cilindro".

3.Altura: A altura de um cilindro é a distância entre os dois planos paralelos que contêm as bases do "cilindro".

4.Superfície Lateral: É o conjunto de todos os pontos do espaço, que não estejam nas bases, obtidos pelo deslocamento paralelo da geratriz sempre apoiada sobre a curva diretriz.

5.Superfície Total: É o conjunto de todos os pontos da superfície lateral reunido com os pontos das bases do cilindro.

6.Área lateral: É a medida da superfície lateral do cilindro.

7.Área total: É a medida da superfície total do cilindro.

8.Seção meridiana de um cilindro: É uma região poligonal obtida pela interseção de um plano vertical que passa pelo centro do cilindro com o cilindro.

Classificação dos Cilindros

1.Cilindro circular oblíquo: Apresenta as geratrizes oblíquas em relação aos planos das bases.

2.Cilindro circular reto: As geratrizes são perpendiculares aos planos das bases. Este tipo de cilindro é também chamado de cilindro de revolução, pois é gerado pela rotação de um retângulo.

3.Cilindro eqüilátero: É um cilindro de revolução cuja seção meridiana é um quadrado.

Àrea do Cilindro

Em um cilindro circular reto, a área lateral é dada por A(lateral)=2pi.r.h, onde r é o raio da base e h é a altura do cilindro. A área total corresponde à soma da área lateral com o dobro da área da base.

Volume do Cilindro

Em um cilindro, o volume é dado pelo produto

da área da base pela altura.

V = A(base) h

Cones

Um cone é um sólido geométrico formado por todos os segmentos de reta que têm uma extremidade em um ponto V (vértice) em comum e a outra extremidade em um ponto qualquer de uma mesma região plana R (delimitada por uma curva suave, a base).

Elementos do cone

1-Base: A base do cone é a região plana contida no interior da curva, inclusive a própria curva.

2-Vértice: O vértice do cone é o ponto P.

3-Eixo: Quando a base do cone é uma região que possui centro, o eixo é o segmento de reta que passa pelo vértice P e pelo centro da base.

4-Geratriz: Qualquer segmento que tenha uma extremidade no vértice do cone e a outra na curva que envolve a base.

5-Altura: Distância do vértice do cone ao plano da base.

6-Superfície lateral: A superfície lateral do cone é a reunião de todos os segmentos de reta que tem uma extremidade em P e a outra na curva que envolve a base.

7-Superfície do cone: A superfície do cone é a reunião da superfície lateral com a base do cone que é o círculo.

8-Seção meridiana: A seção meridiana de um cone é uma região triangular obtida pela interseção do cone com um plano que contem o eixo do mesmo.

Classificação do cone

Quando observamos a posição relativa do eixo em relação à base, os cones podem ser classificados como retos ou oblíquos. Um cone é dito retoquando o eixo é perpendicular ao plano da base e é oblíquo quando não é um cone reto. Ao lado apresentamos um cone oblíquo.

Observação: Para efeito de aplicações, os cones mais importantes são os cones retos. Em função das bases, os cones recebem nomes especiais. Por exemplo, um cone é dito circular se a base é um círculo e é dito elíptico se a base é uma região elíptica.

Esfera

A esfera no espaço R³ é uma superfície muito importante em função de suas aplicações a problemas da vida. Do ponto de vista matemático, a esfera no espaço R³ é confundida com o sólido geométrico (disco esférico) envolvido pela mesma, razão pela qual muitas pessoas calculam o volume da esfera. Na maioria dos livros elementares sobre Geometria, a esfera é tratada como se fosse um sólido, herança da Geometria Euclidiana.

A esfera pode ser definida como "um sólido geométrico formado por uma superfície curva contínua cujos pontos estão eqüidistantes de um outro fixo e interior chamado centro"; ou seja, é uma superfície fechada de tal forma que todos os pontos dela estão à mesma distância de seu centro, ou ainda, de qualquer ponto de vista de sua superfície, a distância ao centro é a mesma.

Uma esfera é um objeto tridimensional perfeitamente simétrico. Na matemática, o termo se refere à superfície de uma bola. Na física, esfera é um objeto (usado muitas vezes por causa de sua simplicidade) capaz de colidir ou chocar-se com outros objetos que ocupam espaço.

Área e volume da Esfera

A área da superfície de uma esfera de raio r é:

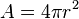
e o volume é:

A esfera tem a menor superfície entre todos os sólidos de dado volume e tem o maior volume dentre todos os sólidos de determinada área. Por isso, a esfera sempre aparece na natureza: bolhas e pequenas gotas d'água, por exemplo, são aproximadamente esféricas, pois a tensão superficial busca uma área superficial mínima.

O cilindro circunscrito numa dada esfera tem um volume igual a 3/2 do volume da esfera, e uma área superficial que é 3/2 da superfície da esfera. Isto, assim como as fórmulas de área e volume acima, já era conhecido por Arquimedes.

Uma esfera pode ser também definida pela rotação de um círculo por qualquer reta que passa por um diâmetro. Se tivermos uma elipse no lugar do círculo, e rotacionarmo-na por um dos eixos, a forma criada será uma esferóide.